Modern Bathroom Vanity, Grey Oak, Black Ceramic Sink, 32 Inch, Free Standing
Nameeks DERIN631
Highlights
Overview
What's Included?
Description
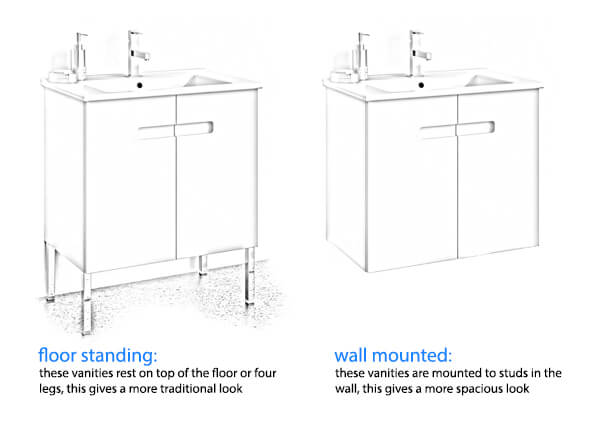
This ultra modern floor standing bathroom vanity set was designed by high-end brand Nameek's. Inspired by modern and contemporary style bathroom design, this bathroom vanity set comes with a beautiful matte black ceramic sink that perfectly fits into a vanity cabinet with two spacious drawers. Ceramic sink features counter space on both sides of the basin. Vanity cabinet is made of durable engineered wood and features two soft-closing drawers with sleek black drawer handles. Vanity cabinet attaches on top of a beautiful black base with four vanity feet. This vanity set is part of the Derin collection. Make a bold statement in your bathroom now with this modern bathroom vanity set.
Product Details
- Vanity cabinet made of engineered wood
- Matte black ceramic sink
- Cabinet features water resistant exterior panels
- Vanity cabinet in grey oak finish
- Black vanity cabinet feet
- Black vanity cabinet handles
- Cabinet features 2 soft-closing drawers
- Faucet not included
- Perfect for modern bathrooms
- Ceramic sink features counter space
- Includes manufacturer 1 year warranty
- Wood grain and color variations are to be expected
Technical Specifications
| Download: | |
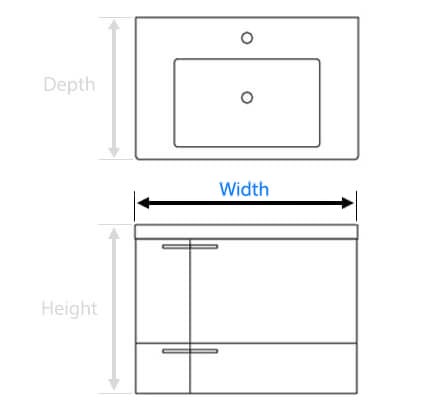
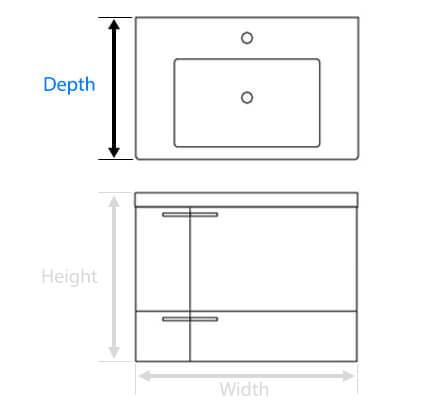
| Overall Width: |
 31.89 Inches
|
| Overall Depth: |
17.32 Inches
|
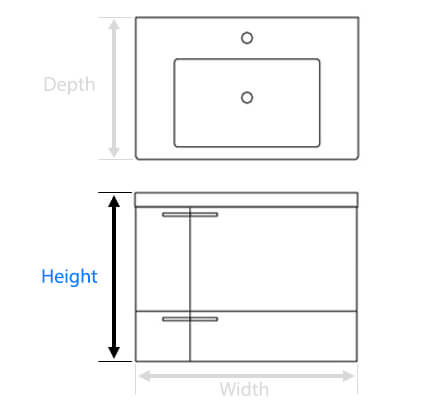
| Overall Height: |
34.65 Inches
|
| Weight: |
140 Lbs
|
| Vanity Cabinet: |
Width: 31.42" Depth: 16.93" Height: 19.69"
|
| Bathroom Sink: |
Basin Depth: 3.6" Basin Width: 12.2" Basin Length: 15.8"
Overall Length: 31.9" Overall Width: 17.4" Overall Height: 5.6" Download Specs |
| Vanity Foot: |
Width: 23.23" Depth: 16.93" Height: 9.45"
|
What's In the Box
3 items
32 Inch Wall Mount Grey Oak Bathroom Vanity Cabinet With Black Handles
Black Ceramic Wall Mounted or Vessel Sink With Counter Space
Scarabeo 5123-49-One Hole
Matte Black Vanity Cabinet Feet
Features
| Sink Finish: |
Matte Black
|
| Top Material: |
Ceramic
|
| Top Finish: |
Matte Black
|
| Color: |
Grey Oak
|
| Style: |
Modern, Contemporary
|
| Installation: |
Floor Standing
|
| Cabinet Material: |
Engineered Wood
|
| Cabinet Finish: |
Grey Oak
|
| Number Of Sinks: |
Single
|
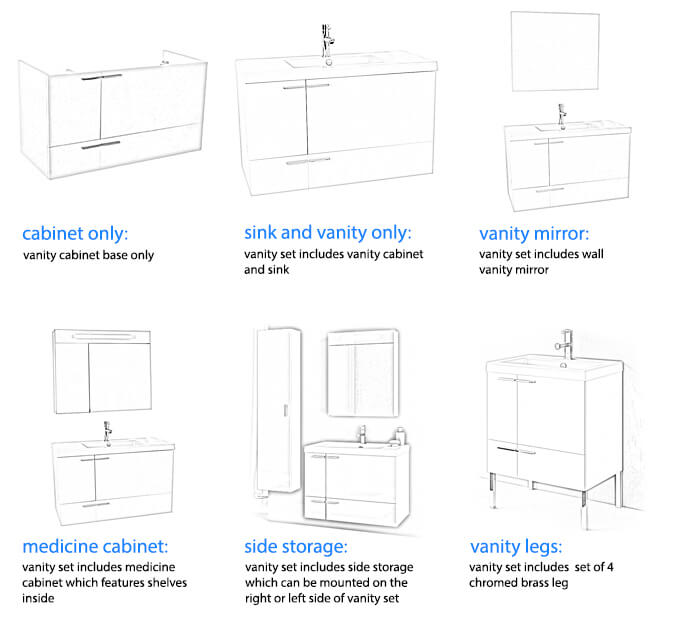
| Pieces Included: |
Sink, Vanity, Sink and Vanity Only, Vanity Cabinet Feet
|
| Handle Finish: |
Matte Black
|
| Application: |
Bathroom
|
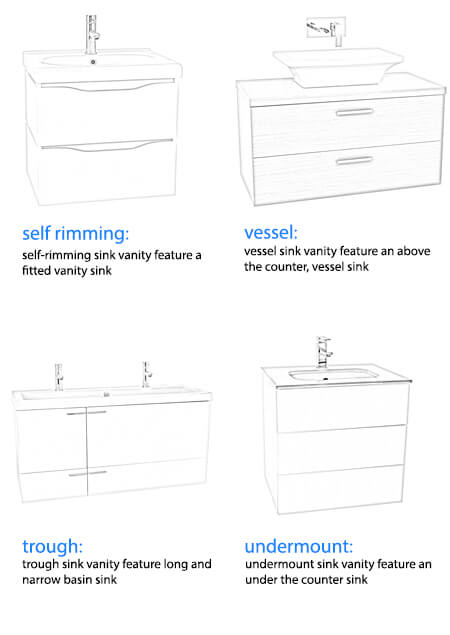
| Sink Type: |
Self Rimming
|
| Mirror Type: |
No Mirror
|
| Features: |
Vanity Legs, Sink and Vanity Only, With Counter Space
|
| Sink Material: |
Ceramic
|
| Type: |
Single
|
| Shape: |
Rectangular
|
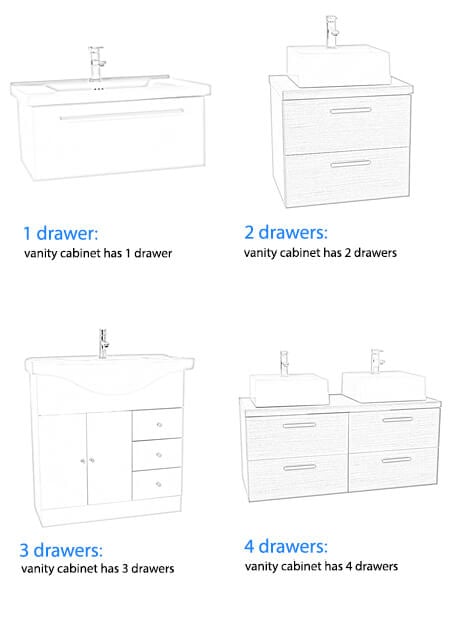
| Drawers: |
2 Drawers
|
| Number Of Pieces: |
3 Piece
|
| Vanity Finish: |
Grey Oak
|
| Vanity Material: |
Engineered Wood
|
| Additional Note: |
Set includes single faucet hole sink. If you would like a no hole or 8 in. widespread configuration, please call in to customize your order.
|
| Soft Close Drawer(s): |
Yes
|
| Cabinet Fully Assembled: |
Yes
|
More Information
| Product Name: | Modern Bathroom Vanity, Grey Oak, Black Ceramic Sink, 32 Inch, Free Standing |
| SKU: | Nameeks DERIN631 |
| Type: | |
| Collection Name: | |
| Brand Name: | |
| Country of Origin: | Europe |
| Categories: | |
| California Prop 65: |
Yes
|
Availability & Shipping
| Availability: | In Stock. |
Items Included
| Vanity Cabinet: |
32 Inch Wall Mount Grey Oak Bathroom Vanity Cabinet With Black Handles.
Nameeks DER31-01
|
| Bathroom Sink: |
Black Ceramic Wall Mounted or Vessel Sink With Counter Space.
Scarabeo 5123-49-One Hole
|
| Vanity Foot: |
Matte Black Vanity Cabinet Feet.
Nameeks NLG02
|
Shipping & Delivery
This item is large and ships with an LTL carrier. Once your order has shipped and is near the vicinity of your area, a representative
from the delivery company will contact you to set up a date and time window for delivery; generally, this is scheduled during normal
business hours. A delivery checklist is provided to ensure you are fully prepared for delivery.
Download Delivery Checklist
Customer Reviews
Sorry, there are currently no reviews for this product.
Product Q/A's
Sorry, there are currently no Q/A's for this product. Do you have a question?
Nameeks Brand Information
Nameek's is a leading designer, developer, and marketer of luxury home & bath products. In cooperation with top European manufacturers, Nameek's choice of designs has become extremely diversified. Nameek's experience in the plumbing industry spans 30 years and today, Nameek's distributes its products throughout the world.
Customers Also Viewed
Related Searches
